Identitât d'Euler
| Cél articllo est ècrit en arpetan supradialèctâl / ORB lârge. |
En matèmatiques, l'identitât d'Euler est una relacion entre plusiors constantes fondamentales et utilisant les três opèracions aritmètiques d'adicion, multiplicacion et exponenciacion :
yô la bâsa e du logaritmo naturèl reprèsente l'analise, l'unitât imaginâ i reprèsente l'algèbra, la constanta d'Archimèdo π reprèsente la géométrie, l'entiér 1 l'aritmètico et lo nombro 0 les matèmatiques.
El est nomâye d'aprés lo matèmaticien Leonhard Euler que la fât aparêtre dens son Introductio, publeyê a Losena en 1748. Devant que d'étre citâye per Euler, ceta formula ére cognessua du matèmaticien angllês Roger Cotes, môrt en 1716.
Dèmonstracion[changiér | changiér lo tèxto sôrsa]
Per l'analise complèxa[changiér | changiér lo tèxto sôrsa]
Vu que cos π = –1 et sin π = 0, ceta formula est lo câs particuliér x = π de la formula d'Euler en analise complèxa (por tot nombro rèèl x, eix = cos x + i sin x). O est asse lo câs particuliér n = 2 porce que la soma des racenes n-ièmes de l'unitât est nula.
Per la geomètrie[changiér | changiér lo tèxto sôrsa]
-
Juxtaposition de 8 triangles rectangles
-
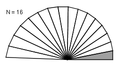
Juxtaposition de 16 triangles rectangles
-
Illustration du résultat
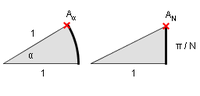
L'entèrprètacion geomètrica que fornét una pista de dèmonstracion per una suite est fondâye sur lo fêt de posar couta a couta des triangllos rèctangllos.
adonc, los multiplicacions complèxes sè traduisent per des rotacions, lo pouent de coordonâs est obtenu en posant couta at couta N triangllos rèctangllos
Biôtât matèmatica[changiér | changiér lo tèxto sôrsa]
L'identitât d'Euler est sovent citâye coment un ègzemplo de biôtât matèmatica.
En èfèt, en ples de l'ègalitât, três des opèracions fondamentales de l'aritmètica y sont utilisâyes, châcuna un côp : l'adicion, la multiplicacion et l'exponenciacion. L'identitât fât asse-ben entèrvenir cinq constantes matèmatiques fondamentales :
- 0, l'èlèment netro de l'adicion.
- 1, l'èlèment netro de la multiplicacion.
- π, tojorn presenta en trigonomètrie, en geomètrie dens la èspâço uclidien et en analise matèmatica (π = 3,14159265...)
- e, bâsa des logarithmes qu'apparait sovent en analise, carcul difèrencièl et matèmatiques financiéres (e = 2,718281828...). Tot coment π, o est un nombro transcendant.
- i, l'unitât imaginâ a la bâsa des nombros complèxos, qu'ant pèrmês l'ètude de la rèsolucion des ècouacions polinomiales devant que de vêre lor usâjo èlargi.
L'enventèro de cetos difèrents èlèments est mielx metu en èvidence per la notacion polonêsa envèrsa de la formula d'Euler :
- 0 ; 1 ; e ; i ;π ; * ; ^ ; +; =
On en dèduit que l'exponenciala complèxa est 2πi-pèriodica.
Notes et rèfèrences[changiér | changiér lo tèxto sôrsa]
Traduccion de l'articllo francês corrèspondent a lo 25 de mê 2022